Spacetime Geometry Inside a Black Hole

by Jim Haldenwang
written Nov. 12, 2004
revised July 30, 2012

This paper describes the nature of spacetime in and around black holes.  Toward the end of the paper, the reader is taken on an imaginary journey inside a black hole.  But first, the reader is introduced to a very elegant theory of space, time, and gravity – Einstein's general theory of relativity.  General relativity gives us the tools we need to understand black holes.  In this paper, I assume the reader is familiar with calculus and special relativity.  We start by reviewing the special theory of relativity, introducing a geometric approach that leads naturally to the general theory.

The Special Theory of Relativity

Special relativity is called "special" because it describes a special type of motion:  uniform, straight-line motion without any acceleration.  Two observers who are in uniform, straight-line motion relative to one another are called inertial observers.  Their frames of reference are called inertial reference frames.  If two observers are accelerating relative to one another, they are not inertial observers, and their situation cannot be handled by special relativity.  Einstein developed special relativity in the year 1905, focusing on inertial observers and ignoring acceleration.  Over the next ten years, he was able to generalize his theory to include all types of motion, including acceleration and gravity.  Einstein published his general theory of relativity in 1916.  (He published his first paper on the subject in November, 1915.)  We will explore the general theory of relativity shortly.

Special relativity is based on two principles.  First is the special principle of relativity, which states that the laws of physics are the same in all inertial reference frames.  This means that there is no absolute rest frame.  One observer's point of view is as valid as another's.  The second principle is Einstein's light postulate, which states that the speed of light in vacuum is constant and has the same value for all inertial observers.  This postulate has been verified by innumerable experiments.  These experiments have always found the same value for the speed of light in empty space, regardless of the (uniform) motions of the measuring devices.  The speed of light in vacuum is about 300,000 km (kilometers) per second.  This speed is represented by the letter c, which stands for celeritas (Latin for "swift").

The constancy of the speed of light runs counter to our ordinary, everyday experience of motion.  Normally when we measure the speed of an object, we measure that speed with respect to something.  For example, if I am walking at 3 miles per hour, it is understood my speed is measured with respect to the ground I'm walking on.  If I walk at 3 mph on a moving train, an observer standing next to the tracks might measure the train's speed to be 60 mph, and my speed as 63 mph.  A passenger sitting in the train would measure my speed to be 3 mph, however.  We say that motion is relative.  Light does not behave like this, however.  If I'm in a spaceship flying away from the Sun at 100,000 km/sec and I measure the speed of the Sun's light rays streaming past me, I will not get a value of 200,000 km/sec, as one might expect.  Instead, the measurement will turn out to be 300,000 km/sec – the same value obtained by observers here on Earth.

In order to understand this curious result, we must take a closer look at what we are measuring when we measure an object's speed.  In order to measure the speed of anything, we divide the distance in space by the amount of time it took to travel that distance.  In other words, we measure speed in units of space divided by time.  So if the speed of light is truly constant for all observers regardless of their relative motions, it must be the units of space and time that change.  Einstein's insight was to realize that space and time are not absolute and unchanging, as previously thought.  Instead, space and time are relative and depend on the motion of the observer.

In his special theory of relativity, Einstein worked out exactly how the units of space and time must vary in order for the speed of light to remain constant for all inertial observers.  For example, suppose two observers, Alice and Bob, both decide to measure the speed of a passing light ray from the Sun.  Alice is in a spaceship zipping away from the Earth and Sun at 150,000 km/s (half the speed of light), while Bob is at rest in his observatory back on Earth.  Both Alice and Bob come up with the same speed for the light ray, namely 300,000 km/s.  They both measured the distance the light ray traveled over some period of time.  In order for Alice's measurement on board her moving spaceship to come out the same as Bob's, Bob concludes that Alice's measuring stick must be shorter than his own, and her stop watch must be running slower than his.  From Bob's point of view, space has contracted in Alice's direction of motion and time for Alice has slowed down or dilated.  Space contracts and time dilates by exactly the amount needed so that when Alice measures the speed of a passing light ray, she obtains the same value that Bob does.  Two handy mnemonics for remembering how space and time change with motion are: "moving sticks are shortened" and "moving clocks run slow."

In order to quantify the amount that space and time change with uniform motion, Einstein introduced a factor called γ (gamma).  In SI (standard international) units of meters (m) and seconds (s), γ is given by

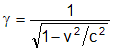
For example, if Alice's spaceship is traveling at half the speed of light, then v = 150,000,000 m/s, so 1 − v²/c² = 1 − (150,000,000 m/s)² / (300,000,000 m/s)² = 0.75, and so γ = 1/√(0.75) ≈ 1.15.  To determine the length of Alice's measuring stick relative to Bob, we divide by γ.  If her measuring stick is one meter long when she is at rest, then the length of Alice's stick when she is moving at half the speed of light is, according to Bob, 1 m / 1.15 = 0.87 m.  According to Alice, however, her stick is still exactly one meter long.  To determine how much slower her clock runs relative to Bob, we multiply by γ.  Since 1 s × 1.15 = 1.15 s, Bob finds that Alice's clock runs about 15% slower than his.

In general relativity, SI units are not very convenient to work with.  Instead, we use what are known as "geometrized units."  With geometrized units, we measure both distance and time in meters.  To convert time from seconds to meters, we ask, how long does it take light to travel a distance of one meter?  Since light travels 300 million meters in one second, light travels one meter in just one 300-millionth of a second.  One meter of time is equal to 1/300,000,000 s.  In geometrized units, the speed of light is 1 and dimensionless, since light travels 1 meter of distance in 1 meter of time (c = 1 m / 1 m = 1).  Geometrized units are much more convenient to work with in relativity theory.  Also, as we shall soon see, relativity treats space and time much alike, so it is appropriate to use the same units for both.

If we substitute c = 1 into the formula for γ given above, we obtain γ in geometrized units:

Returning to our example of Alice and Bob, we can now calculate γ using geometrized units.  Since the spaceship is traveling at half the speed of light, v = 0.5, so 1 − v²  =  1 − (0.5)² = 0.75, and γ = 1/√(0.75) ≈ 1.15, the same result we obtained earlier.

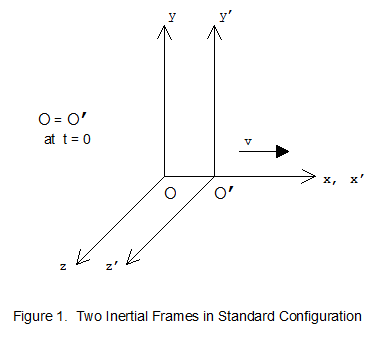
In relativity theory, we often work with two coordinate systems (reference frames) that are in motion relative to one another.  Each coordinate system represents spacetime as experienced by one of the observers.  Since spacetime has four dimensions (three of space and one of time), we need to specify four coordinates.  If we know the coordinates of a point in one coordinate system, say (t, x, y, z), we may want to know the coordinates of that point in the other coordinate system.  In Newtonian mechanics, we can find these other coordinates, say (t′, x′, y′, z′), by using the Galilean transformation.  Consider two observers O and O′, where O′ moves with constant velocity v along the positive x axis of a Cartesian coordinate system, and the positions of O and O′ coincide with the origin at time t = 0.  See figure 1.  In this configuration (known as the standard configuration), the Galilean transformation is given by

t′ = t,   x′ = x − vt,   y′ = y,   z′ = z.

In special relativity, the Galilean transformation will not work.  This is because of time dilation and spatial contraction.  Notice, for example, how the time coordinate does not change in the Galilean transformation, even though the two coordinate systems are in motion relative to one another.  This reflects the Newtonian world view, in which time is absolute and unchanging.  In special relativity, the Galilean transformation is replaced by the Lorentz transformation.  In geometrized units, the Lorentz transformation is given by

t′ = γ(t − vx),   x′ = γ(x − vt),   y′ = y,   z′ = z. (1)

The Lorentz transformation can be derived by applying the special principle of relativity and the light postulate to two coordinate systems in the standard configuration described above.

In Euclidean geometry, we measure the spatial distance Δd between two objects or events by using the Pythagorean theorem:

Δd²  =  Δx² + Δy² + Δz² ,

where Δx, for example, is the change in x, that is, the difference between the x coordinates of two events.  Suppose, for example, that Alice and Bob are playing catch.  Bob throws the ball to Alice.  Let's refer to the place and time where Bob throws the ball as event P and the place and time where Alice catches it as event Q.  We can designate the x coordinate of event P as x_P and the x coordinate of event Q as x_Q.  Then Δx = x_Q − x_P.  Similarly, Δy = y_Q − y_P and Δz = z_Q − z_P.  Using the Pythagorean theorem, we can compute Δd, the distance between these two events.

In Newtonian mechanics the Pythagorean theorem is used to measure the distance or spatial separation between two events.  The distance Δd is frame-invariant, which means that two Newtonian observers in relative motion to one another will always obtain the same value when they measure the distance between two events.  In order to prove that the Pythagorean distance is invariant under the Galilean transformation, we start with

and replace x′, y′ and z′ using the Galilean transformation.  For example,

After completing these algebraic manipulations, the reader can verify that

which shows that the distance is frame-invariant under the Galilean transformation.  The Pythagorean distance is not invariant under the Lorentz transformation, however.  This is because in special relativity, spatial distances can vary for observers who are moving relative to one another.

Although Einstein found that space and time measurements can vary in different reference frames, his math teacher Minkowski found a way to measure space and time together in such a way that the measurement does not vary.  This discovery was of fundamental importance to the subsequent development of general relativity.  Minkowski replaced the Euclidean distance with the spacetime interval.  The frame-invariant spacetime interval Δs between two events is defined by

Δs² = −Δt² + Δx² + Δy² + Δz² .

Unlike ordinary distance, the spacetime interval measures the separation between two events in both space and time.  In order to prove that the spacetime interval is invariant under the Lorentz transformation, we start with

and replace t′, x′, etc. using the Lorentz transformation, as given above (1).  After some algebraic manipulations, the reader can verify that

which shows that the interval is frame-invariant.  Minkowski's discovery allows us to use the spacetime interval in place of the theorem of Pythagoras in order to measure "distance" (spacetime separation) in the non-Euclidean geometry of special relativity.

What does the frame-invariance of the spacetime interval really mean?  Minkowski said:  "From henceforth, space by itself, and time by itself, have vanished into the merest shadows and only a kind of blend of the two exists in its own right."  Consider a three-dimensional object, say a stick.  It casts a two-dimensional shadow against a wall.  As we turn the stick about, the length of the shadow changes, even though the stick itself remains the same length.  In an analogous fashion, we can imagine a four-dimensional spacetime "object."  All inertial observers agree that this object has the same "length" (interval) in spacetime.  However, different observers see different lengths for the three-dimensional "shadow" of the object in space.

Using the spacetime interval and geometrized units, we can classify the separation between two events in one of three ways:

1.  If Δs² < 0, the events are said to have timelike separation.  For any two events with timelike separation, the separation in space is less than the separation in time.  To see this, consider the following:

which shows that Δd < Δt.  In this case, it is possible for one inertial observer to experience both events.  We say the events lie on the world line of such an observer.  The observer is traveling slower than the speed of light, since Δd/Δt < 1.

2.  If Δs² = 0, the events are said to have null or lightlike separation.  In this case the events lie on the world line of a light ray.  The separation in space and the separation in time are equal.  (Δd = Δt,  or  Δd/Δt = 1, the speed of light in geometrized units.)

3.  If Δs² > 0, the events are said to have spacelike separation.  Two events with spacelike separation cannot lie on the same world line, since Δd/Δt > 1 (greater than the speed of light).  In this case there always exists some inertial reference frame in which the events are simultaneous (separated in space but not in time).

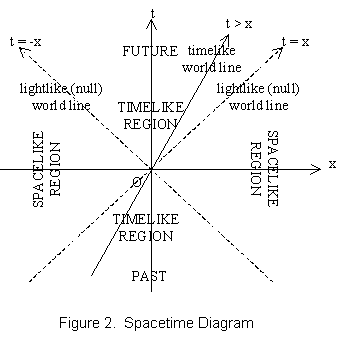
In special relativity, the paths of material particles are restricted to timelike world lines, and the paths of photons (light rays) are restricted to null or lightlike world lines.  Spacelike world lines are excluded.  (Spacelike world lines correspond to paths that are faster than the speed of light, or that go backward in time.)  See figure 2.  In this diagram, the vertical axis t represents time and the horizontal axis x represents one dimension of space.  The origin O represents the present moment for some observer.  The observer's future lies somewhere between the two lightlike world lines, with t > 0.  The observer's past lies somewhere between these two world lines, with t < 0.  If we were to add a dimension by adding a y axis perpendicular to the x and t axes, the lightlike world lines would form two cones meeting at the origin.  These are called "light cones."

When two events have timelike separation (Δs² < 0), we define the proper time interval between the events to be Δτ (delta tau), where

The proper time, also known as the wristwatch time, is the time measured by an observer who experiences both events.  Since the proper time for lightlike world lines is zero, we can say that photons do not experience the passage of time.  (Δτ = |Δs| = 0 for photons.)

Let's consider the spacetime interval of a photon traveling in the x direction.  For this photon, Δy and Δz are zero.  Setting Δs² = 0, we obtain

0  =  −Δt² + Δx² or

so that

which is the result to be expected.  In all inertial frames of reference, the speed of light is constant and equal to one in geometrized units.

As another example, let's consider the case of the twin sisters, Mary and Jane.  Jane decides to travel to the nearest star, Alpha Centauri.  She has at her disposal a very fast spaceship, one that can travel almost as fast as light.  Her sister Mary is somewhat of a homebody, however, and prefers to stay on Earth.  Let's compare the proper times of the two sisters, using Mary's reference frame for our calculations.  We ignore acceleration in this example, for which we would need to use general relativity.  Also, instead of meters, we use years for t and light-years for x.

Mary says good-bye to Jane and waits 12 years.  After 12 years, Jane returns from her journey to Alpha Centauri, 4.5 light-years away.  Mary calculates her own proper time interval as follows:

Since she stayed at home, she used Δx = 0 in her calculation.

Mary is surprised to find that Jane has not aged as much as her, however.  She is not so surprised after calculating Jane's proper time interval.  Using Δx = 9 light-years, she obtains:

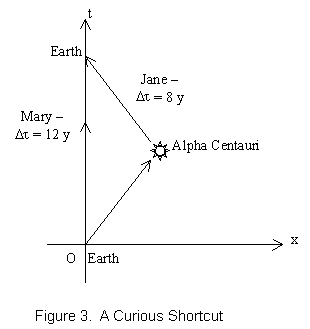
See figure 3.  Again, this calculation is only approximately correct, since no adjustment was made for the time Jane spent accelerating and decelerating.  However, this example illustrates an interesting fact:  the longest path through Minkowski spacetime is actually the one that involves no movement through space, only time.  This is because we subtract the spatial components of the path in order to compute the interval.  Minkowski spacetime (our spacetime!) is truly non-Euclidean in character.

The General Theory of Relativity

Special relativity does not take acceleration into account.  Acceleration occurs whenever an observer changes her speed or direction of motion.  In 1907, Einstein had what he called "the happiest thought of my life," that the effects of acceleration cannot be distinguished from the effects of gravity.  Einstein called this the principle of equivalence.  For example, suppose you are traveling in a spaceship far away from any planet.  Suppose the rockets fire, causing the spaceship to accelerate forward at a rate of 10 m/s².  You would soon find yourself on the "floor" of the spaceship (the rear bulkhead).  You would experience a force which could not be distinguished from gravity.  You could stand up and walk around the rear bulkhead, and it would feel the same to you as if you were walking around on the Earth.

Once Einstein realized that the effects of gravity and acceleration are equivalent, he was able to extend the principle of relativity from inertial reference frames to all reference frames.  He did this by showing that the laws of physics that describe acceleration could also be used to describe gravity.

In order to understand how Einstein made use of his principle of equivalence, imagine a playground merry-go-round (the type children grab onto and run next to in order to build up speed and then jump onto).  When the merry-go-round spins around, any children on board will experience an outward-directed force, called centrifugal force.  Now imagine placing hundreds of toothpicks on the merry-go-round, forming a series of concentric rings, some near the center of the merry-go-round, some out near the edge, and some in between.  Imagine the toothpicks are glued in place and arranged so that they all point in the direction of the merry-go-round's rotation.  Now imagine standing next to the merry-go-round and watching it spin around, with the concentric rings of toothpicks whirling around with it.  By special relativity, since the toothpicks are in motion relative to you, they will become shorter ("moving sticks are shortened").  The toothpicks near the outside of the merry-go-round move fastest, so they contract the most.  Just as the toothpicks are shortened, so space itself is shortened or warped.  Next, replace the toothpicks with small clocks, hundreds of them all over the merry-go-round.  Now when the merry-go-round whirls around the clocks run slower, with the ones near the outside running more slowly than the ones near the center.  Time slows down on the merry-go-round, especially near the outer edge.  Thought experiments like this showed Einstein that spacetime must be warped in the presence of acceleration.  And since he believed that acceleration is equivalent to gravity, Einstein saw that spacetime must also be warped in the presence of gravity.  He soon came to believe that matter and energy cause spacetime to warp, and this warping of spacetime is what we experience as gravity.

According to Einstein, a kid on a merry-go-round is traveling through warped spacetime, which she experiences as centrifugal force.  She is attempting to follow a path through warped spacetime that leads away from the merry-go-round.  Similarly, our travels through the warped spacetime near planet Earth cause us to experience the force we call gravity.  (And note that even when we are standing still, we are still traveling through time, so we still feel the force of gravity.  We are always moving through spacetime.)  With these insights to guide him, Einstein went on to develop his general theory of relativity.

General relativity is Einstein's theory of gravity.  It is founded on two core principles:  (1) The principle of equivalence:  the effects of acceleration and the effects of gravity are essentially equivalent.  (2) The general principle of relativity:  the laws of physics are the same in all reference frames, including accelerating frames.  An accelerating frame of reference without gravity is equivalent to a non-accelerating frame with gravity.  For example, the occupant of an accelerating car is pressed back against his seat.  Alternatively, the occupant could choose to view himself as stationary while the rest of the universe accelerates past him.  From this alternative viewpoint, the gravitational field of the rest of the universe accounts for the force he experiences pressing him back against his seat.  General relativity tells us that these two viewpoints are equivalent.

General relativity is a geometric theory.  Gravity is no longer treated as a force of attraction between two bodies.  Instead, gravity is associated with the warping of space and time.  The warping or curvature of spacetime is caused by massive objects such as stars or planets.  In fact, according to general relativity, matter, energy, and pressure all cause spacetime to warp.

How does the warped spacetime around Earth cause objects to fall toward it?  Free-falling objects in a gravitational field follow geodesics, which are paths of extremal length.  They are either the longest or the shortest possible paths between any two points in spacetime.  According to general relativity, free-falling objects take the longest possible paths through spacetime, so they follow geodesics.  We perceive free-falling objects in a gravitational field to be falling because they are following geodesics through curved spacetime.

Light rays also follow geodesics, but these geodesics cannot be defined in terms of length, since all lightlike paths have the same length (spacetime interval), namely zero.  Instead, we define these geodesics as the straightest possible paths through curved spacetime.  This definition is made precise through the techniques of differential geometry, the generalized non-Euclidean geometry developed in the 19th century by the great mathematicians Gauss and Riemann, and utilized by Einstein in general relativity.

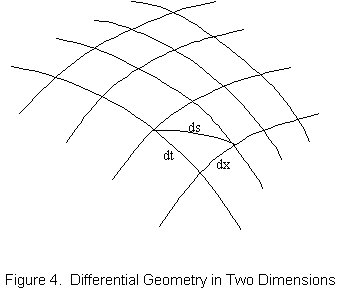
In differential geometry, a curved surface is divided up into an infinite number of infinitesimally small pieces.  Each piece is measured by the "metric" or "line element" ds, a differential which gives the distance between two points that are infinitesimally close together on the surface.  See figure 4.  The techniques of differential geometry can be used to find an equation for the metric that is valid anywhere on the curved surface.  Unlike conventional geometry, with differential geometry distances can be determined on a curved surface without reference to anything outside of the surface.  For example, if we consider a sphere as a two-dimensional curved surface, the circumference of the sphere can be determined without knowing its radius, which lies outside the surface of the sphere.

The techniques of differential geometry will work in general, for any continuous curved surface whatsoever, in any number of dimensions.  Just what Einstein needed for his theory of gravity.

In general, in the four dimensions of spacetime, the equation for the metric assumes the following form:

ds² = g₁₁ dt² + g₂₂ dx² + g₃₃ dy² + g₄₄ dz²

+ 2 g₁₂ dt dx + 2 g₁₃ dt dy + 2 g₁₄ dt dz + 2 g₂₃ dx dy + 2 g₂₄ dx dz + 2 g₃₄ dy dz. (3)

The ten coefficients g_αβ are, in general, functions of t, x, y and z.  In three-dimensional Euclidean space, we set

g₂₂ = g₃₃ = g₄₄ = 1,

and the other coefficients equal to zero.  We then obtain the conventional Pythagorean formula

ds² =  dx² + dy² + dz²,

which measures the distance between two infinitesimally close points in Euclidean space.  To find the distance Δs between two points a finite distance apart, we sum up the differentials by integrating the metric along the geodesic connecting the two points.  Of course, in Euclidean space we know the geodesic is just the straight line connecting the two points, and we don't have to use integration to find the distance.  However, the technique of taking the line integral of the metric along the geodesic between two points to find the distance between them will work in any geometry whatsoever, Euclidean or non-Euclidean, flat or curved.

The general formula for the metric given above (3) can be called the generalized Pythagorean theorem for four-dimensional spacetime.  In the flat Minkowski spacetime of special relativity, we set

g₁₁ = −1,     g₂₂ = g₃₃ = g₄₄ = 1,

and the other coefficients equal to zero.  We then obtain the Minkowski metric

ds² = −dt² + dx² + dy² + dz². (4)

By integrating this metric along the world line connecting two events in flat (Minkowski) spacetime, we can find the interval Δs between the events.  Again, there are easier ways to find the interval in flat spacetime, but in the curved spacetime of general relativity, taking the line integral of the metric is the only way that will always work.

When gravity or acceleration is present, spacetime becomes warped, so the formula for the metric becomes more complex than the ones used for Euclidean or Minkowski space.  We will see an example of such a metric shortly, when we discuss black holes.

According to general relativity, the metric ds is frame-invariant.  We can use it to find the interval between two events in any frame of reference, no matter what motion or acceleration may be present.  In order to change from one reference frame to another, however, the coefficients g_αβ must be transformed (using an appropriate transformation formula).  The value of ds is not changed by this transformation, even though the coefficients of the metric do change.

Along with differential geometry, general relativity uses a mathematical tool called tensor analysis.  Tensors are real-valued, multi-dimensional functions of vectors.  They are useful because they are frame-invariant.  In other words, a tensor will give the same real number regardless of the reference frame in which the vector components are calculated.  This property makes tensors a useful short-hand for representing the frame-invariant metrics of general relativity.

In general relativity, a tensor representing the curvature of spacetime is set equal to a tensor representing the stress-energy content of spacetime (the matter, energy and pressure present).  This is the way that general relativity mathematically models the concept that matter, energy and pressure cause spacetime to warp, which we experience as gravity.  This tensor equation can be written as

G^αβ = 8π T ^αβ ,

where G and T are the tensors representing the curvature and the stress-energy content of spacetime, respectively.  This equation is the most important result of general relativity.  It can be used to construct mathematical models of the universe, as well as of stars and black holes.  The expansion of this tensor equation gives the "Einstein field equations," a system of ten non-linear partial differential equations.  These cannot be solved in general.  Instead, initial conditions and simplifying assumptions, such as spherical symmetry, are used to obtain a simpler, solvable set of equations.  When these equations are solved, the result is the metric tensor, which contains the ten coefficients g_αβ of the metric (3).  The resulting metric describes the geometry of the spacetime being modeled (for example a star, a black hole, or the universe).  (With simplifying assumptions, some of the ten coefficients will be zero.)

In the simplest case, that of flat spacetime (no acceleration or gravitational field), the metric tensor expands to give the Minkowski metric (4).  When the methods of general relativity are applied to a curved spacetime geometry (such as we find inside or near a star), the result is a more complex metric.

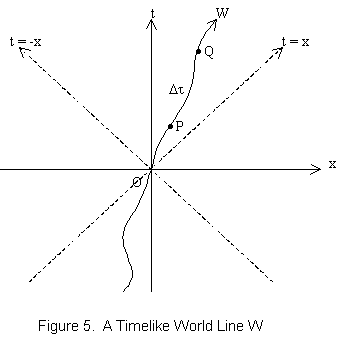
In general, the proper time interval between two infinitesimally close events on a timelike world line can be obtained from the metric by finding dτ = |ds|.

The proper time interval Δτ between two events P and Q that lie on a timelike world line W is defined to be the line integral of dτ along W from P to Q.  See figure 5.  In general relativity, world lines can be curved due to acceleration or gravity, but the slope must remain less than 45 degrees (in geometrized units).

The proper time Δτ from P to Q is equal to the time measured on a clock that moves along W from P to Q.  (This is known as the Clock Hypothesis.)

Our experience of physical reality tells us that time has a direction.  We assume that it is not possible for an observer to travel along the world line W from Q to P (backward in time).

The Schwarzschild Metric

In 1915, the German physicist Karl Schwarzschild solved the Einstein field equations for the special case of a spherical, non-rotating mass (such as a star or black hole).  The so-called Schwarzschild metric can be used to describe the curvature of spacetime caused by a non-rotating black hole.  The Schwarzschild metric was derived using the reference frame in which the spherical object is stationary.  This means that the coefficients of the Schwarzschild metric are valid only for observers who are "at rest" or motionless relative to the object.  "At rest" means that the spatial coordinates of these observers do not change over time.

The Schwarzschild metric can be applied only to non-rotating black holes.  A solution for rotating black holes was found by Kerr.  As the Kerr metric is more complex, this paper will only consider the Schwarzschild metric.  (Most of the results given here are valid for Kerr's solution, also.)

Consider a black hole of mass M (in geometrized units), centered at a point r = 0.  For r > 2M, the Schwarzschild metric is given in spherical coordinates (t, r, θ, φ) by

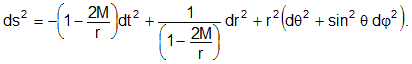
There are many interesting and surprising features of the geometry described by this metric.  First I mention that the "radius" r = 2M is called the Schwarzschild radius or event horizon of the black hole.  The event horizon can be thought of as the boundary that separates the inside from the outside of a black hole.

As r approaches 2M, the coefficient of dt² approaches zero and the coefficient of dr² approaches infinity (since 1 − 2M/2M = 1 − 1 = 0).  For a long time, it was not known whether the infinite "singularity" at r = 2M was a real, physical singularity which could not be passed through by an infalling observer, or just a coordinate singularity.  (A familiar example of a coordinate singularity is the one at r = 0 in polar coordinates, where θ can take on any value and is therefore indeterminate.  A transformation to Cartesian (rectangular) coordinates eliminates this singularity.)  In general, a coordinate singularity indicates a mathematical problem, not a real, physical problem, and can be eliminated by a coordinate transformation.

Although the singularity at r = 2M was long suspected to be a coordinate singularity, this was not proved until the late 1950s, when a coordinate transformation was found that eliminated the singularity.  Additional coordinate transformations have been discovered since.  These will not be considered here, as they are mathematically complex.

In the subsequent analysis, we will often consider the perspective of an observer who is at rest at "infinity," that is, very far away from the black hole.  For such an observer, the proper time and the coordinate time are almost equal.  To see this, consider the Schwarzschild metric, given above.  As r approaches infinity, the coefficient of dt² approaches −1.  The spatial coordinates r, θ, and φ for a resting observer are constant over time, so the differentials dr, dθ, and dφ are zero.  Therefore, dτ = |ds| ≈ dt.  Hence, the proper time Δτ of an observer at rest far from a black hole is approximately equal to the coordinate time Δt. 

By setting ds² = 0 in the Schwarzschild metric, we can study the behavior of a light ray near the event horizon, as seen by an observer at rest at "infinity."  We can simplify the analysis by assuming the ray travels along a radial null geodesic, either directly toward the black hole or directly away from it.  Then the θ and φ coordinates of the light ray do not change.  This implies that dθ and dφ are zero, so we can eliminate the right-hand term in the Schwarzschild metric.  Setting ds² = 0, we have

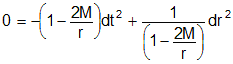
so that

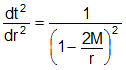or

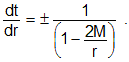
Now as r approaches 2M, dt/dr approaches infinity.  This is a time dilation effect.  Any message sent via light signal from near the event horizon (r = 2M) to an observer far from the black hole will be stretched out or dilated.  The closer the emitter of the light signal is to the event horizon, the more stretched out the message will appear to the far-away observer.  The frequency of the light signal decreases, or redshifts, because lower frequency light carries less information per unit of time (the far-away observer's wristwatch time).  The closer to the event horizon the light signal is sent from, the greater is the redshift observed from far away.  When the emitter is very close to the event horizon, the observed redshift is so great that the light signal disappears altogether.  For this reason, the event horizon is sometimes called the infinite redshift horizon.

Taking the reciprocal, we see that dr/dt approaches 0 as r approaches 2M.  Since we solved the Schwarzschild metric for a radial lightlike geodesic (by setting ds² = 0), dr/dt corresponds to the speed of light.  Hence the speed of light approaches 0 as r approaches 2M, relative to an observer far from the black hole.  At r = 2M, an outward-directed light ray is frozen in time and space, and never reaches an observer at r > 2M.

Since we said that the speed of light is constant in special relativity, one might ask how the speed of light can vary in general relativity.  The answer is that gravitational fields change the geometry of spacetime, and the speed of light is fundamentally tied to the nature of the spacetime geometry the light is passing through.

According to general relativity, matter, energy and pressure cause spacetime to bend, stretch or compress.  Light rays follow geodesics through this bent, stretched or compressed spacetime.  The warping of spacetime warps the paths of the light rays.

Relative to an observer at rest far from a black hole, space is compressed (contracted) near the event horizon and time is stretched out (dilated).  Each meter of space is shorter compared to the space far from a black hole, and each meter of time is longer.  Relative to the far-away observer, a light ray, traveling through one meter of space in one meter of time, travels a short distance in a long time.  To the far-away observer, the light ray has slowed down.

Although the speed of light can vary in general relativity, it is still always the case that material objects cannot attain or exceed this speed.

Inside the Black Hole

Now let's consider the Schwarzschild solution for 0 < r < 2M (inside a black hole).  A small but very important change must be made to the metric for this case.  When r > 2M, the coefficient (1 − 2M/r) is positive.  However, for 0 < r < 2M, this coefficient is negative.  In order to work with positive coefficients for this case, we use

The metric then becomes

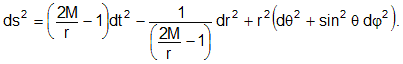
Notice how the minus sign has moved from the t coordinate to the r coordinate.  This means that inside the event horizon, r is the timelike coordinate, not t.  In relativity, the paths of material particles are restricted to timelike world lines.  Recall the discussion of timelike separation earlier in this paper (2).  It is the coordinate with the minus sign that determines the meaning of "timelike."  According to relativity, inside a black hole time is defined by the r coordinate, not the t coordinate.  It follows that the inevitability of moving forward in time becomes, inside a black hole, the inevitability of moving toward r = 0.  This swapping of space and time occurs at r = 2M.  Thus, r = 2M marks a boundary, the point where space and time change roles.  For the observer inside this boundary, the inevitability of moving forward in time means that he must always move inward toward the center of the black hole at r = 0.  All timelike and lightlike world lines inside r = 2M lead inevitably to r = 0 (the end of time!)  Because it is not possible for any particle or photon inside r = 2M to take a path where r remains constant or increases, the boundary r = 2M is called the event horizon of the black hole.  No observer inside the event horizon can communicate with any observer outside the event horizon.  The event horizon can be thought of as a one-way boundary.

Earlier, we showed that the speed of light approaches zero near the event horizon, relative to an observer far from the black hole.  This means that the far-away observer can never see an infalling observer reach or cross the event horizon, because any light radiating from the infalling observer slows down and redshifts, with the redshift approaching infinity as the infalling observer nears the event horizon.  Does this mean that the infalling observer does not actually reach or cross the event horizon?  No.  The infalling observer does in fact cross the event horizon.  Remember that the singularity at r = 2M (the event horizon) was shown to be a coordinate singularity, not a real, physical singularity.  Using transformed coordinates, it can be shown that the infalling observer passes from r > 2M to r = 0 in a finite amount of time (his proper time, or the interval along his world line).

Furthermore, it can be shown that the maximum amount of proper time from r = 2M to r = 0 available to an observer who has fallen through the event horizon, even if he has at his disposal a rocket of unlimited power, is given by

Δτ  ≤  π M  meters,

where M is the geometrized mass used in the Schwarzschild metric.  M is related to the Newtonian mass m by

M = Gm/c² ,

where G is the gravitational constant in SI units.  The mass of the Sun is 1,477 meters in geometrized units.

Let's look at a real-life example.  Astronomers believe there is a supermassive black hole at the center of our galaxy, with a mass about 4.3 million times the mass of the Sun.  The tidal force near the event horizon of such a large black hole is weak.  (The tidal force, or tidal acceleration gradient, is the difference in the gravitational acceleration between two points in a non-uniform gravitational field.  The smaller the black hole, the larger this gradient is near the event horizon, because the curvature of spacetime is greater.  An astronaut approaching a stellar-sized black hole only a few times the mass of the Sun would be torn apart by the tidal force before reaching the event horizon.)  Since the tidal force near the supermassive black hole is weak, it is possible that an astronaut, if well-protected from radiation, could survive to cross the event horizon and continue inward.  Let's calculate the maximum time this astronaut could avoid reaching the center of the black hole.  (For simplicity, we'll assume the black hole is not rotating, so the above formula can be used.)

Δτ  ≤  π M  =  π × 4,300,000 × 1,477 meters  =  2.0 × 10¹⁰ meters  =  67 seconds.

Our intrepid astronaut has only about one minute to explore the black hole!  The Schwarzschild radius of this black hole is

r  =  2M  =  2 × 4,300,000 × 1,477 m  =  12.7 million km.

The Center of the Black Hole

What happens at r = 0?  In the Schwarzschild metric, the expressions 2M/r approach infinity as r approaches 0.  This is a real, physical singularity, not a coordinate singularity.  All the mass of a Schwarzschild black hole is concentrated at r = 0, a point of infinite density, where space and time come to an end.  The presence of real singularities in solutions of the Einstein field equations suggests that general relativity is an incomplete theory of gravity.  Physicists are leery of theories that predict infinities.  None of the dials on their gauges can register infinite values!  It seems likely that general relativity does not accurately describe what happens at r = 0.

Where might general relativity have a problem?  One of the assumptions underlying general relativity is that spacetime is continuous.  This can be seen in the usage of differential geometry as the mathematical basis of the theory.  Differentials measure infinitesimally small distances, which only makes sense if spacetime is continuous.  It may be that spacetime is actually discrete, or quantized, with a smallest possible size.  Physicists are exploring this idea as they work on new theories of quantum gravity.  If this idea is correct, then the differential equations of general relativity are only approximations of reality.  These approximations are valid in the large, even down to the atomic level, but at some point they break down.  The smallest possible unit of spacetime is thought to be near the Planck length, an incredibly tiny 10⁻³⁵ m.  This is twenty orders of magnitude smaller than the nucleus of an atom.  Such small sizes are not currently accessible to science.  To the precision our instruments can now measure, general relativity has been found to be accurate.

A viable theory of quantum gravity must combine general relativity with quantum mechanics.  Such a theory must match the predictions of general relativity on large scales, since these predictions have proven to be accurate.  Quantum gravity can deviate significantly from general relativity only on the smallest of scales.  The core concept of general relativity is that gravity is spacetime curvature.  A future theory of quantum gravity must honor this concept.  Somehow, a quantum of gravity (a graviton) must be related to a quantum of spacetime.  A successful theory of quantum gravity will be a successful theory of quantized spacetime (or vice versa).  The harmonious merging of quantum mechanics with general relativity is perhaps the greatest problem facing theoretical physicists today.  If and when a way is found to accomplish this task, we may learn what really happens at the center of the black hole!

Real black holes almost certainly rotate.  Such black holes can be modeled by the Kerr metric, a more complex metric whose detailed analysis is outside the scope of this paper.  The interested reader should consult Taylor and Wheeler's fine book, Exploring Black Holes: Introduction to General Relativity.   The Kerr black hole does not have a point singularity at r = 0.  Instead, the singularity has a ring structure, and can be avoided by most trajectories.  In theory, a particle that avoids the ring singularity can pass through r = 0 to a region where r < 0.  It is unlikely that such a region physically exists.  It is more likely that general relativity does not correctly describe the nature of real black holes at r = 0.  A future theory of quantum gravity should provide us with a more realistic description of the center of the rotating black hole.

Physical Interpretation of the Event Horizon

We found earlier that the Schwarzschild metric has a coordinate singularity at the event horizon, where the coordinate time t becomes infinite.  Yet a calculation using transformed coordinates shows that an infalling observer reaches and passes through the event horizon in a finite amount of time (his proper time).  How can we understand the nature of a place where time seems to be both finite and infinite? 

Far from the event horizon, the coordinate t approximates an observer's proper time or wristwatch time.  This leads us to think of the coordinate t as representing time.  This is not true at the event horizon, however.  As an infalling observer nears the event horizon, the coordinate t has less and less to do with time as he perceives it – that is, his proper time.  In order to understand how time is perceived by the infalling observer, we need to focus on his proper time and ignore the coordinate t.

Even though we can never actually see someone fall through the event horizon (due to the infinite redshift), he really does.  As the free-falling observer passes through the event horizon, any inward-directed photons emitted by him continue inward toward the center of the black hole.   Any outward-directed photons emitted by him at that instant are forever frozen at the event horizon.  So the far-away observer cannot detect any of these photons, whether directed inward or outward.

Life Inside the Black Hole

Some have speculated that our universe might exist inside a gigantic black hole.  Let's explore this idea further, in order to gain more insight into what the interior of a black hole is really like (and for the fun of it).  If our universe is inside a giant black hole, one might ask where the event horizon is.  Is there any path we can take that will bring us closer to the event horizon?  According to general relativity, if our universe is inside a black hole, every point in our universe is moving closer to the center of this black hole, and away from the event horizon.  There is no (spatial) direction that will bring us closer to the event horizon.  As it is difficult to visualize a four-dimensional curved surface, subtracting a dimension or two makes it easier.  Imagine a giant sphere, and a point on the interior surface of this sphere. This point detaches from the inner surface and moves toward the center, at the same time expanding into a disk.  This expanding disk represents our universe expanding in space as it moves through time.  In this model let's suppose that our universe formed on the event horizon of the giant black hole, represented by the surface of the sphere.  We suppose that the Big Bang occurred at the event horizon of the black hole.  See figure 6.  The expanding disk is a two-dimensional representation of the three spatial dimensions of our universe.  (We could label these spatial dimensions θ, φ, and t.)  Every point in our universe (the disk) is moving away from the inner surface of the sphere (the event horizon) toward the center of the sphere (the singularity of the giant black hole).  The dimension through which this disk is moving is a timelike dimension (which we could label r).  For every point on the disk (our universe at a point in time), the event horizon lies in the past and the singularity of the black hole lies unseen in the future.  All timelike and lightlike world lines in our universe lead from the event horizon to the singularity of the black hole.  To travel to the event horizon would be to travel backward in time.  Therefore, there is no path we can take that will bring us closer to the event horizon.

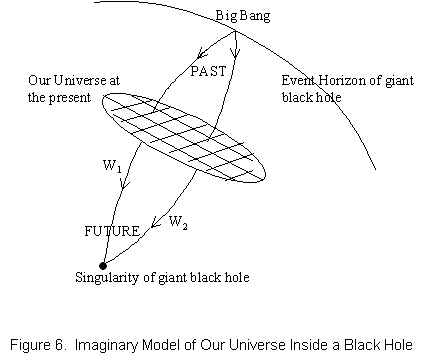
In this imaginary model, the only point of the spacetime of our universe that is connected to the event horizon of the giant black hole is the point in space and time at which the Big Bang occurred.  With a powerful enough telescope, one can, in theory, look in any direction and see the Big Bang (or at least 380,000 years after the Big Bang, when the universe became transparent).  One can look around in any direction and see the Big Bang, yet one cannot travel toward it, because it lies in the past.  This is the way of things inside any black hole.  Even a super-powerful rocket cannot prevail against the gentle timelike acceleration toward the singularity at the center of a black hole.  The event horizon lies in the past of any observer inside a black hole, and the central singularity lies in his future.

If we lived inside a gigantic black hole, could we detect it?  If we had sensitive enough instruments, it might be possible to detect the tidal acceleration gradient, at least over astronomical distances.  This might be mistaken for a slight variation in the strength of gravity over very large distances.  Also, the expansion of the universe might eventually slow down and reverse, as we move closer to the central singularity of the black hole.  In this model, our universe would eventually shrink down to a single point (the Big Crunch).

Recommended Reading:

• Einstein's Theory of Relativity:  M. Born  (Dover, 1965).
• A History of Mathematics:  C. B. Boyer  (Wiley, 1991).
• Relativity: The Special and the General Theory:  A. Einstein  (Crown, 1952).
• The Fabric of the Cosmos:  B. Greene  (Random House, 2004).
• Quantum Non-Locality and Relativity (Third Edition):  T. Maudlin  (Wiley-Blackwell, 2011).
• A First Course in General Relativity:  B. F. Schutz  (Cambridge, 1990).
• Exploring Black Holes: Introduction to General Relativity:  E. F. Taylor and J. A. Wheeler  (Addison Wesley Longman, 2000).
• Black Holes and Time Warps: Einstein's Outrageous Legacy:  K. Thorne  (W. W. Norton, 1995).

Back to Jim's Science Page